Particle Swarm Art: Reconstructing images with particle swarm optimization

We talk a lot about AI today and it’s usually LLMs all the way down. But there’s a whole playground of “older” techniques that still delight. This weekend project uses Particle Swarm Optimization (PSO) to reconstruct an image using nothing but semi‑transparent triangles, live in your browser.

Try the demo

👉 https://adamstirtan.github.io/particle-swarm-painter

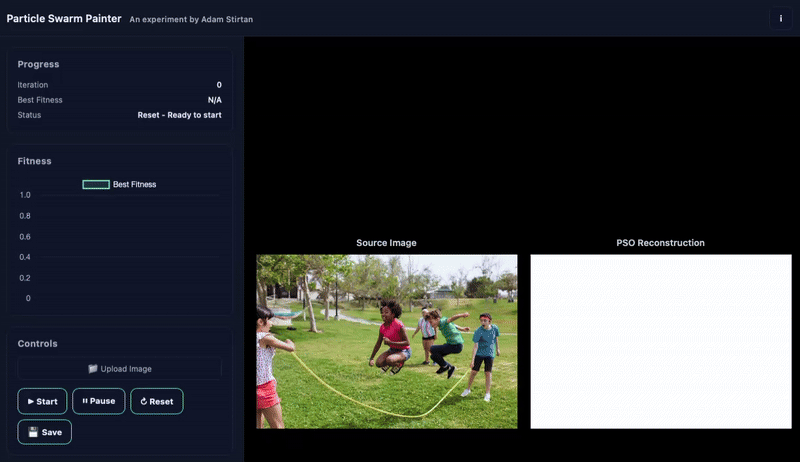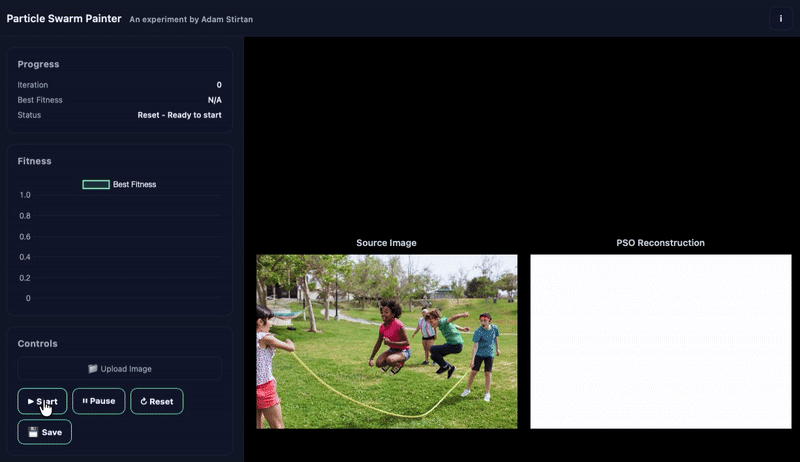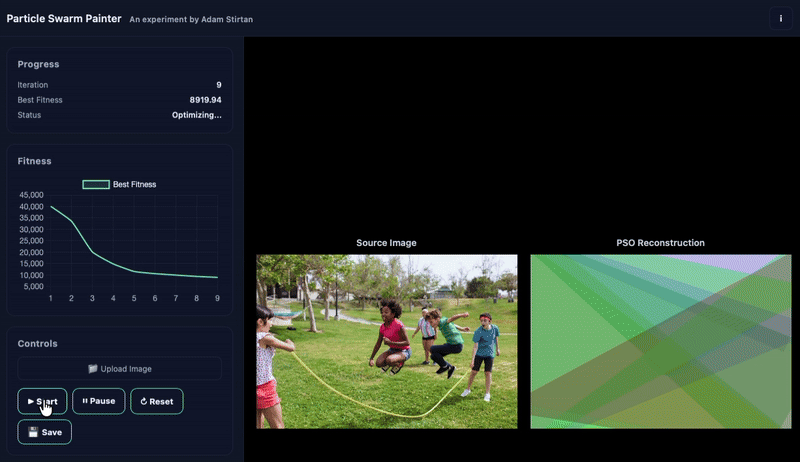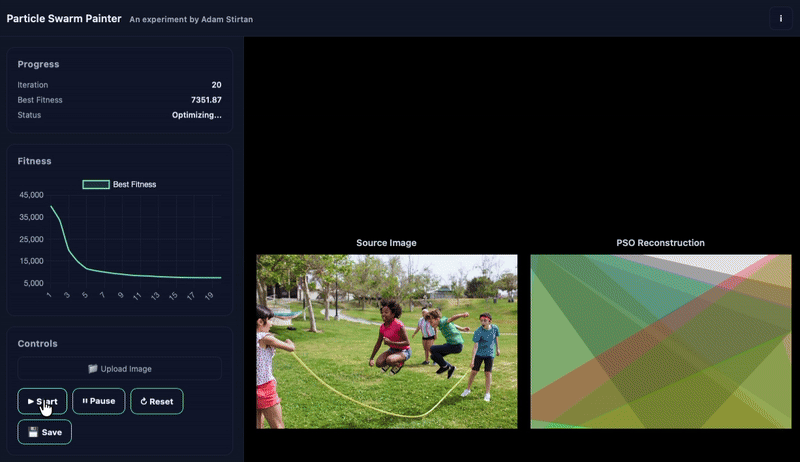
Upload an image to be drawn using triangles. I suggest a simple photo of a person, perhaps yourself? You could use the default parameters or play with them. I have set the defaults to something that works. Allow the algorithm to work for about 1000 iterations. Squint your eyes to see the reconstruction taking shape during early iterations.

How it works

• Representation: A solution of N triangles. Each triangle = 10 parameters (three points + RGBA)
• Fitness: Render those triangles to an offscreen canvas, compare pixels to the source image and measure error. Lower is better.
• PSO: A swarm of candidate solutions “fly” through the search space. Each iteration updates velocities using inertia (w), personal attraction (c1) and social attraction (c2) towards the global best.
• Guardrails that matter:
  • Max alpha clamps triangle opacity so one opaque shape doesn’t dominate. The result is layered, painterly blending. Try a lower value.
  • Offscreen margins let triangles extend beyond the canvas a bit; this creates nicer edges and compositions.
  • Stagnation detection optionally grows the number of triangles if progress stalls. More triangles = more expressive capacity, but we add them thoughtfully, not all at once.

Core loop

function step() {
  for (const particle of swarm) {
    for (let i = 0; i < particle.params.length; i++) {
      const r1 = Math.random(),
        r2 = Math.random();
      particle.v[i] =
        w * particle.v[i] +
        c1 * r1 * (particle.pbest[i] - particle.x[i]) +
        c2 * r2 * (gbest[i] - particle.x[i]);
      particle.x[i] += particle.v[i];
    }
    clampTriangleParams(particle.x, { maxAlpha, bounds, margin });
    particle.fitness = evaluateFitness(particle.x, sourceImageData);
    if (particle.fitness < particle.pbestFitness) updatePersonalBest(particle);
  }
  updateGlobalBest(swarm);
  maybeHandleStagnationAndTriangleGrowth();
}

Fitness

Render triangles to an offscreen canvas, grab imageData and compute average per-pixel squared error across RGB channels versus the source.

function evaluateFitness(triangles, sourceData) {
  const rendered = renderToOffscreen(triangles);
  let error = 0;
  for (let i = 0; i < sourceData.data.length; i += 4) {
    const dr = rendered.data[i] - sourceData.data[i];
    const dg = rendered.data[i + 1] - sourceData.data[i + 1];
    const db = rendered.data[i + 2] - sourceData.data[i + 2];
    error += dr * dr + dg * dg + db * db;
  }
  return error / (sourceData.data.length / 4);
}

Stagnation and triangle growth

Sometimes the swarm stalls. We track improvement over a window. If improvement dips below a threshold, we nudge capacity by adding a few triangles. It’s a gentle “more paint on the brush,” not a reset. There’s also a simple kick to re‑seed the worst particles if things get sleepy.

Why the sliders matter

• Swarm size: exploration budget. Bigger is better… until it’s not. Start modest.
• Inertia (w): Momentum. Higher = more wandering; lower = more focus.
• c1/c2: Balance “me vs we.” If c1 dominates, particles overfit their own best; if c2 dominates, they herd too tightly.
• Max Alpha: The painterly secret. Lower values force layers and texture.
• Increase triangles on stagnation: Off by default? Turn it on when you want quality over speed.

What I learned

Small constraints, like the maximum alpha being reduced produce better art. This is because opaque triangles dominant the color space and don’t really exist in real life. Using offscreen margins help composition more than you think. If everything is simply constrained to the canvas, it looks forced. Stagnation heuristics are “free” wins. Gains come from adding more triangles to better represent the image so computations increase linearly with the maximum triangles. Focus on modifying the stagnation criteria for long-tailed gains. Perhaps dynamically adjusting the criteria would improve later generation images.